TP n°3 - Circuits logiques
1ère année maturité
Tout le contenu vu durant les TP fait partie entière de la matière à connaître lors d'évaluation.
Vous avez la possibilité de rendre votre TP à la fin des deux périodes pour obtenir une rétroaction sur votre travail.
Objectifs
- Identifier, nommer et décrire les différents composants d'un circuit logique.
- Illustrer comment à partir de signaux électriques, on simule du code binaire.
- Construire et analyser un circuit logique.
Les composants électroniques d'aujourd'hui ne mesure seulement que quelques nanomètres. Donc pour comprendre le fonctionnement des circuits logiques implémentés dans nos ordinateurs, nous allons utiliser un simulateur.
Simulateur complet : ici.
Voici un circuit logique à 2 entrées et une porte logique ET.
Le menu de gauche vous donne accès à des composants.
Le menu du haut vous permet d'annuler des manipulations, de remettre l'état initial du circuit, de charger un circuit précédemment sauvé, de sauvegarder un circuit ou encore de capturer l'image de votre circuit
Cette activité vous permet simplement de découvrir comment utiliser le simulateur.
- Modifiez les entrées A et B, en cliquant dessus, pour observer la sortie S.
- Affichez la table de vérité en survolant la porte.
- Déplacez les éléments avec la souris.
- Effectuez un clic droite sur la porte et modifiez-la en une porte OR.
- Supprimez le fil entre la porte OU et la sortie en S.
- Ajouter des portes pour créer un circuit correspondant à
(A+B) • A
Un circuit logique est la combinaison de plusieurs portes logiques. Les composants sont eux-mêmes composés de circuits.
Voici un circuit logique à 2 entrées.
Il combine trois types de porte différentes.
- Écrivez la table de vérité de ce circuit, en vous aidant du simulateur.
- Comparer cette table avec le OU. Quelle est la différence?
- Trouver le nom de la porte logique et son symbole qui est équivalente à ce circuit.
Cette fonction s’appelle XOR, et en français «ou exclusif» (OU-X)...
Son expression formelle s'écrit A⊕B et est l'équivalent de AB + AB
Sa table de vérité est alors:
| A | B | S |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
A partir du comportement que doit avoir un composant, on peut écrire sa table de vérité et créer le circuit à l'aide des portes logiques de base.
Equation canonique : S = ABC + ABC
Tout comme en algèbre, on nomme les différents éléments de l'équation des termes. Attention, l'opérateur + est bien le OU logique. Les termes de l'équation représentent tous les cas où la fonction de sortie S vaut 1.
Dans un terme, toutes les entrées sont indiquées sous forme vraies ou fausses (ex: A ou A).
Cette équation peut alors implémenté le circuit correspondant, sans toute fois être le circuit le plus simple.
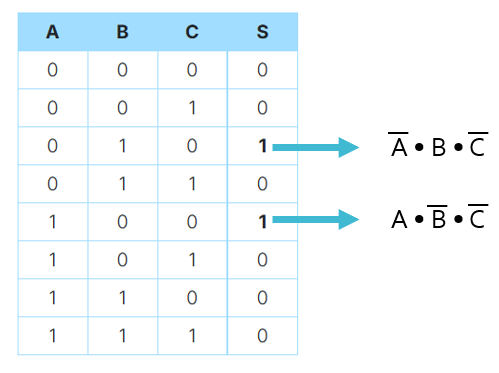
Dans cet exemple, seules deux lignes de la table de vérité sont intéressantes car la sortie S est à 1. On peut alors construire les deux termes correspondant avec les entrées A, B et C.
L'équation canonique est donc : S = ABC + ABC
On peut alors déjà à ce stade construire un circuit fonctionnel répondant à cette table de vérité comme suit:

S = C (AB + AB) on reconnait ici le OU-exclusif
S = C (A ⊕ B)
Ce qui donne le circuit simplifé de droite ci-dessous. On appelle ces deux circuits des circuits équivalents.Vous pouvez les tester.
| Catégorie | Règle | Forme |
|---|---|---|
| Identité | Identité OU | A + 0 = A |
| Identité ET | A · 1 = A | |
| Dominance | Dominance OU | A + 1 = 1 |
| Dominance ET | A · 0 = 0 | |
| Idempotence | Idempotence OU | A + A = A |
| Idempotence ET | A · A = A | |
| Commutativité | OU | A + B = B + A |
| ET | A · B = B · A | |
| Associativité | OU | A + (B + C) = (A + B) + C |
| ET | A · (B · C) = (A · B) · C | |
| Distributivité | ET sur OU | A · (B + C) = AB + AC |
| OU sur ET | A + (B · C) = (A + B)(A + C) | |
| Complément | Complément OU | A + A = 1 |
| Complément ET | A · A = 0 | |
| De Morgan | Négation d’un ET | A · B = A + B |
| Négation d’un OU | A + B = A · B | |
| Absorption | Absorption OU | A + (A · B) = A |
| Absorption ET | A · (A + B) = A |
| A | B | C | S |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
Un circuit logique est souvent complexe, car les informations sont encodées sur plusieurs bits, voire plusieurs octets.
On va donc trouver des circuits avec plusieurs entrées et plusieurs sorties pour représenter cela.
Voici un circuit logique à 3 sorties.
- Avec quels signaux la sortie S2 est-elle obtenue ? Observez bien le circuit.
- Complétez la table de vérité de ce circuit, en vous aidant de la réponse précédente.
| A | B | C | S2 | S1 | S0 |
|---|---|---|---|---|---|
| 0 | 0 | 0 | |||
| 0 | 0 | 1 | |||
| 0 | 1 | 0 | |||
| 0 | 1 | 1 | |||
| 1 | 0 | 0 | |||
| 1 | 0 | 1 | |||
| 1 | 1 | 0 | |||
| 1 | 1 | 1 |
Contexte : Vous devez concevoir un système de sécurité pour une maison. Ce système a trois capteurs :
- Un capteur de porte (A) : signal à 0 si la porte est ouverte
- Un capteur de fenêtre (B) : signal à 0 si la fenêtre est ouverte
- Un capteur de mouvement (C) : signal à 1 si un mouvement est perçu
Le système doit déclencher une alarme (sortie S) si :
- la porte est ouverte
- OU la fenêtre est ouverte
- ET il y a un mouvement détecté
Étapes:
- Définir la table de vérité
- Construire le circuit dans le simulateur
Synthèse à retenir
Pour terminer ce TP, résumez ce que vous avez appris, de la manière que vous préférez (description, carte mentale, schéma, ...).
Pour vous aider, répondez à ces questions.
- Quelles portes logiques connaissez-vous, et lequelles sont strictement nécessaires ?
- Qu'est-ce qu'un circuit logique ? Quand/où est-ce utilisé en informatique ?
- Entrées, sorties, signaux: que veulent dire ces termes ?
- A quoi sert une table de vérité et comment écrit-on les valeurs des entrées ?
- Comment passe-t-on d'une table de vérité à un circuit logique ?